高腳樓房承受超載重發生挫屈之三維分析

                 王慶忠  技師

摘要

本研究探討有耐震能力的RC造高腳樓房，其承受超載活載重時，發生挫屈的可能性。該樓房之梁柱構架樓板系統以三維有限元素模型組成，各個桿件與樓板均切割成元素，梁柱元素勁度矩陣由線性矩陣及幾何矩陣二部分相加，板元素為線性矩陣。特別是各個桿件之挫屈分析不須事先考慮有效長度，三維結構整體之側移(sidesway)狀態不須事先判定。並提出案例驗證探討挫屈分析之可用性。

建模方法

模型建立過程，先設計為均勻斷面尺寸，梁柱板幾何尺寸與材料參數資料。由地面層直接向上延伸，直至設定之頂層，建模同步計算梁柱板之自重，以便求出呆載重(W)及相對應地震側向力(C x W)。

 建模後全數點線面資料取出，將梁柱板分別切割為有限元素，同時將自重與倒三角分配地震側向力，分別由各層樓板面，以垂直與平行方向之節點載重置於各元素節點。地面層為地梁加淺基礎，柱底與地梁交會點以鉸支承模擬。

初步設計

結構用途為工廠作業空間較大之6層樓，X-向跨度9+10+8m，Z-向跨度8+9m，共12支立柱。混凝土抗壓強度210 kg/cm²，柱斷面尺寸55x55cm，梁斷面45x55，板厚20。1FL高6.5米，2~6FL每層4.5米，承受DL自重(另加120kg/m²) 及LL活載重，及EQ地震力。 設計時LL=500kg/m²，水平地震力EQ=0.09W，柱主筋比最大約3.5%，大梁主筋上限0.5平衡比。經有限元線性分析，在1.2DL+0.5LL+1.0EQ載重組合之下，求得各元素內力，各樓層之柱與大梁各斷面均符合安全設計。已先假設小梁的設計與分析不納入模型。圖1為有限元模型。

挫屈分析

分析模型之斷面參數使用有效勁度係數，係考慮混凝土微裂及構架側向載重的效應，故柱與梁有效慣性矩Ieff值，參照規範考量均暫取為0.5Ig。

第一階段為垂直載重下之線性勁度分析，包括呆載重及活載重，取得各柱軸向力。第二階段用軸向力更新各柱勁度矩陣，由線性加幾何勁度[1]組成，總勁度矩陣以高斯消去法作位移分析[2]及二次彎矩計算。

案例探討

分析過程接近挫屈載重時，整體結構勁度矩陣之行列式值<= 0.，及該矩陣消去分解後，在矩陣對角線項出現<= 0.。

驗證1：懸臂柱，斷面正方受軸向載重(P)到達臨界力Pcr (理論有效長度比=2)時，分析得雙向橫方向可同時挫屈，且總勁度矩陣呈非正定(non-positive definite)。

驗證2：懸臂梁，受軸載重及橫向載重一起作用，分析得挫屈前之桿件彎矩=主要彎矩+二次彎矩。

現取初步設計之6層樓結構，作三組模型(柱設計不更動)參數研究 ，並且逐次倍數的增加垂直向活載重，另加側向(Z)水平橫力=0.1 EQ ，可檢視二次彎矩的效應。

Case T20：20公分原板厚+原設計梁。

Case T12：12公分厚度板+原設計梁，以模擬鋼承板。

Case T25：20公分原板厚+ 25公分深度梁，以模擬無梁板。

圖2顯示2FL最大位移(Z向)反應。

Case T25X：側向水平橫力改為 X方向，再次模擬無梁板。

圖3顯示2FL最大位移(X向)反應，直到結構發生挫屈。

結果與討論

三組案例當中，柱尺寸維持不變，只改變梁或板的尺寸，同時各樓層的活載重為均佈，各組的活載重亦對應一致。

1.無梁板情況時，活載重超過呆重約2倍起，P-delta效應開始危險放大。

2.對於柱的側向挫屈支撐而言，梁深度較板厚度更重要。

3.有地震力設計的RC造高腳樓房，其柱與梁系統有相當挫屈抵抗能力。

4.此分析程序增修後，可供探討STEEL造高腳樓房的挫屈可能性。

參考文獻

1.謝元裕，結構穩定學，文笙書局，再版88年4月

2.S.S.Rao，The Finite Element Method in Engineering，Butterworth-Heinemann Co. 3^rd Edition，1999.

圖1 節點化有限元模型

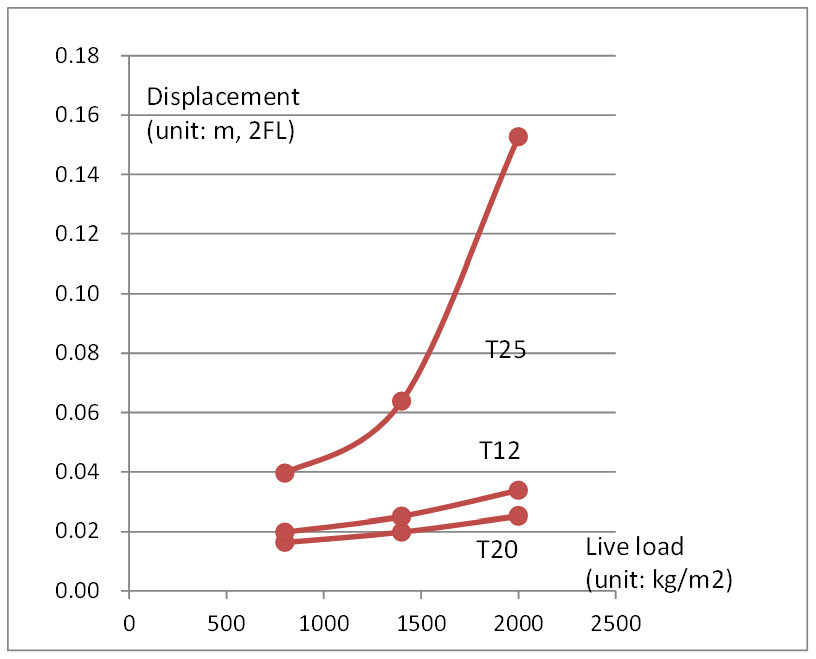圖2 梁板尺寸差別之超載反應

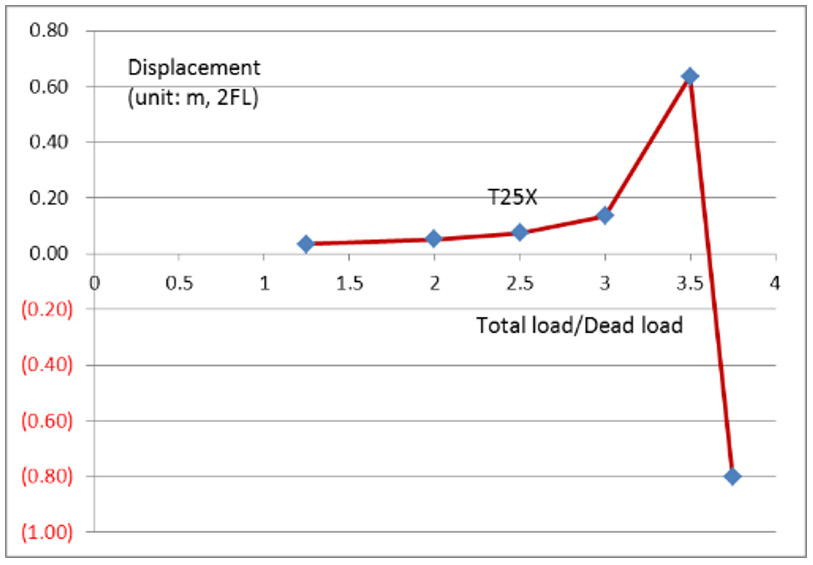圖3 超載至挫屈(Total TL=LL+DL)