矩形能量應用於幾何非線性
呂啟明 技師
本報1194、1224與1235期,分別介紹矩形能量基本概念與其應用,於材料非線性之單雙層門架,本文再談矩形能量於幾何非線性(Geometric Nonlinear)之應用。幾何非線性,一般區分為大應力(Large Stress)與大變位(Large Displacement)效應,大應力效應即我們常說的P-Delta效應,其主要是因在大應力作用下,由於其側向位移(lateral displacement),不管該位移很大或小,均會造成對整體結構的影響。以下就矩形能量應用於P-Delta效應,舉例分析。
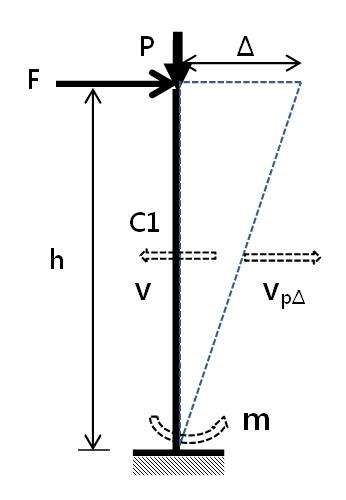
以懸臂立柱如下圖1為說明,外內系統矩形能量平衡式1,成對變相如式2,柱頂受P壓力(向下),則P力因側向變位Δ所造成的彎矩如式3,再除以柱高h,得水平剪力如式4,值得注意的是,透過此轉換,將垂直壓力轉成水平剪力,此P-Delta剪力,與原內彎矩對應的剪力強度方向相反,因此力平衡式改為式5,表示剪力強度因此減少,對應的能量改為式6,表示能量容量受損。
|  |
| 圖1 懸臂立柱 |

以案例1之懸臂立柱說明,其結構示意如圖1,除增加因靜載活載引起之柱頂軸壓力P,為10ton(向下)外,其餘結構條件,均與本報1194期案例A2.0相同。同樣地,分別利用LCM(LuChiMan綠奇門,Ref.-1)、與CSI (ETABS程式,Ref.-2)等兩方法,求取立柱之容量曲線(柱頂位移與基底剪力)。
1.LCM(LuChiMan綠奇門)方法:
本例LCM分析方法,同本報1194期案例A2.0,僅列出各階段柱軸力如表1,其中柱軸力維持固定值,依據前述公式4,計算P-Delta反向剪力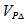 如表2,合併BaseV得水平剪力容量減少,如表2第4列。
如表2,合併BaseV得水平剪力容量減少,如表2第4列。
表1 各階段柱軸力
| Δ= | 0 | 5.972 | 12.452 | 11.727 | 31.155 |
| C1 | -10 | -10 | -10 | -10 | -10 |
表2 懸臂立柱之容量曲線資料
| 2F | Δ= | 0 | 5.972 | 12.452 | 11.727 | 31.155 |
| 1F | BaseV= | 0 | 5 | 5 | 1.67 | 1.67 |
| C1 | VPD= | 0 | -0.17 | -0.35 | -0.33 | -0.87 |
| | BaseV+VPΔ= | 0 | 4.83 | 4.65 | 1.34 | 0.8 |
圖2中之淺綠虛線,原始僅考慮材料非線性之容量曲線(本報1194);而綠色實線,則其再考慮P-Delta效應所得者,可看出因柱頂受壓而水平剪力容量下滑減少趨勢。
|  |
| 圖2 懸臂立柱之容量曲線圖形(LCM) |
2.CSI(ETABS程式)方法:
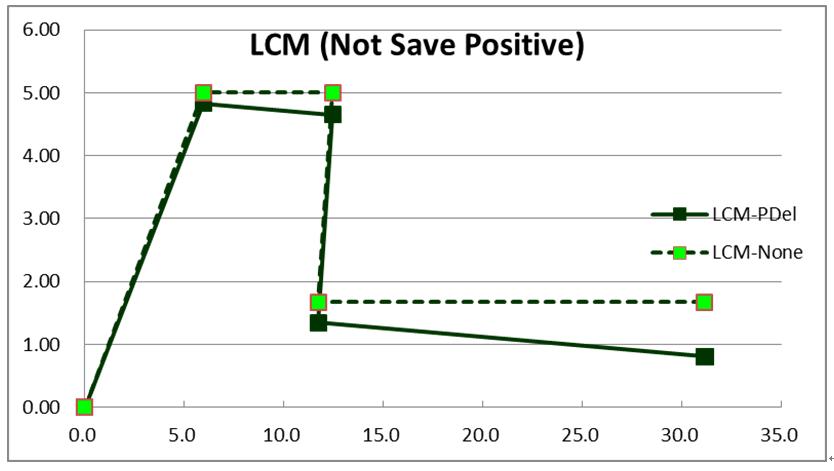
CSI結構模型如圖3,同理將垂直力與水平力各指定為一種Case,例如SLG與SLX,如圖3為SLG-Case,SLX-Case同1194期案例A2.0。同樣地,先跑彈性分析,再依序跑SLG與SLX等兩靜力非線性側推分析,但SLX-Case須將SLG-Case設為從前次Case開始(Start from Previous Case),意即在跑水平側力前,垂直力已經存在,SLG-Case亦需記得加入P-Delta效應。側推得門架容量曲線,如圖4中之紅色圓形實線,另外紅色圓形虛線,為原始僅考慮材料非線性之容量曲線(本報1194期)。
|  | | 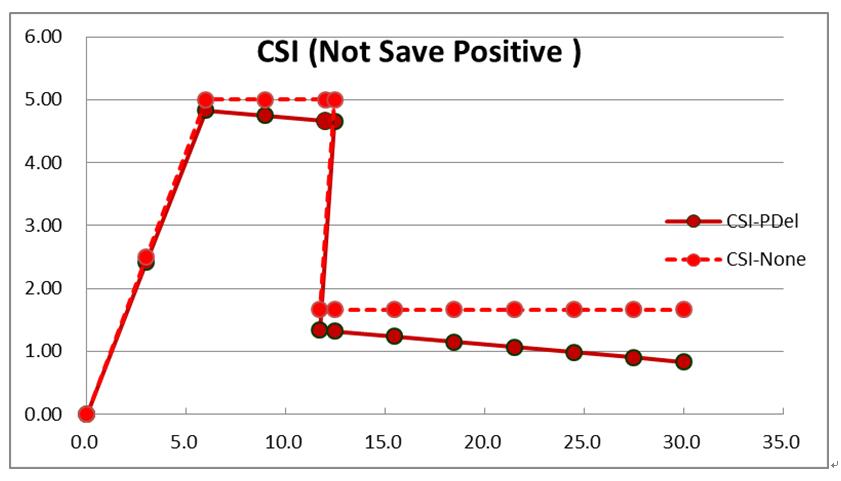 |
| 圖3 懸臂立柱之結構模型圖(CSI) | | 圖4 懸臂立柱之容量曲線圖形(CSI) |
比較LCM與CSI等容量曲線如圖5,兩者完全重合,表LCM理論驗證可行。
| 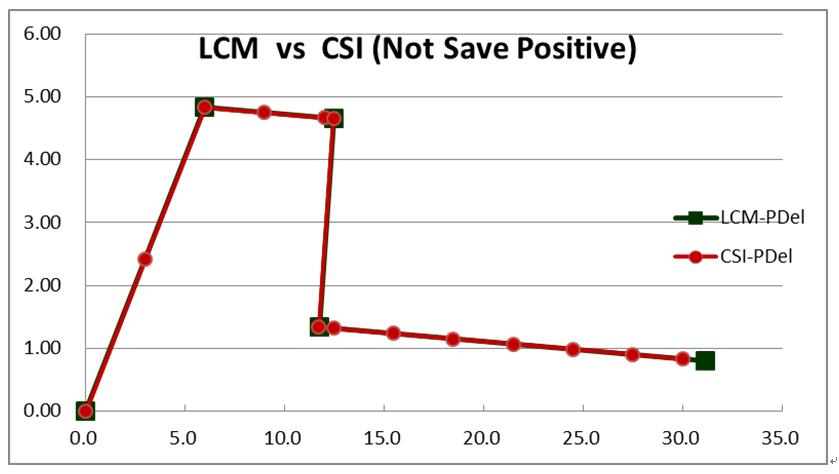 |
| 圖5 懸臂立柱之LCM與CSI比較 |
再舉案例2,雙層門架說明,其結構示意如圖6,除增加因靜載活載引起之各柱頂軸壓力10ton外,其餘結構條件均與本報1235期(第3篇)案例1相同,同樣地分別利用LCM與CSI等兩方法,求取本門架之容量曲線。
| 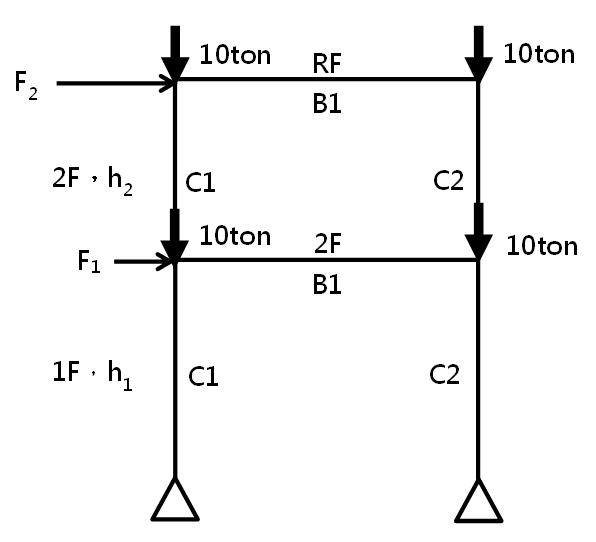 |
| 圖6 案例2之結構系統 |
1.LCM(LuChiMan綠奇門)方法:
本例LCM分析方法,同本報1235期之案例1,僅列出各階段柱軸力如下表3,其中柱軸力不再維持固定值,依據公式4,計算P-Delta反向剪力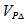 如表4,合併原始基底剪力(Base Shear),得表4最後一列。
如表4,合併原始基底剪力(Base Shear),得表4最後一列。
表3 雙層門架之各階段柱軸力
| Drift-RFL | 0 | 0.927 | 0.927 | 0.31 | 0.31 |
| 2FC1_Top | -9.25 | -6.65 | -6.65 | -8.88 | -8.88 |
| 2FC2_Top | -10.75 | -13.35 | -13.35 | -11.12 | -11.12 |
| Drift-2FL | 0 | 6.646 | 13.126 | 13.753 | 31.379 |
| 1FC1_Top | -20 | -8.8 | -8.8 | -16.26 | -16.26 |
| 1FC2_Top | -20 | -31.2 | -31.2 | -23.74 | -23.74 |
表4 雙層門架之容量曲線資料
| RFL | Dis.RF | 0 | 7.566 | 14.046 | 12.261 | 31.686 |
| 2FC1_Top | VPD= | 0 | -0.021 | -0.021 | -0.009 | -0.009 |
| 2FC2_Top | VPD= | 0 | -0.041 | -0.041 | -0.011 | -0.011 |
| 1FC1_Top | VPD= | 0 | -0.162 | -0.321 | -0.621 | -1.417 |
| 1FC2_Top | VPD= | 0 | -0.576 | -1.138 | -0.907 | -2.069 |
| Base Shear | VBS= | 0 | 10 | 10 | 3.34 | 3.34 |
| Base Shear | VBS+VPD= | 0 | 9.2 | 8.48 | 1.79 | -0.17 |
圖7中之淺綠虛線為原始僅考慮材料非線性之容量曲線(本報1235期),而綠色實線則其再考慮P-Delta效應所得者,可看出因柱頂受壓而水平剪力容量下滑減少趨勢。
| 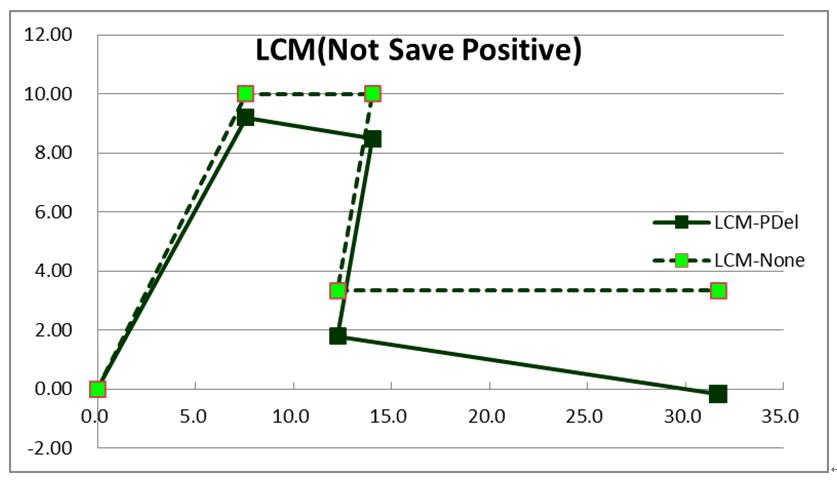 |
| 圖7 雙層門架之容量曲線圖形(LCM) |
2.CSI(ETABS程式)方法:
CSI結構模型如圖8,同前例先跑彈性分析,再依序跑SLG與SLX等兩靜力非線性側推分析,側推得門架容量曲線,如圖9中之紅色圓形實線,另外紅色圓形虛線,為原始僅考慮材料非線性之容量曲線(本報1235期)。
| 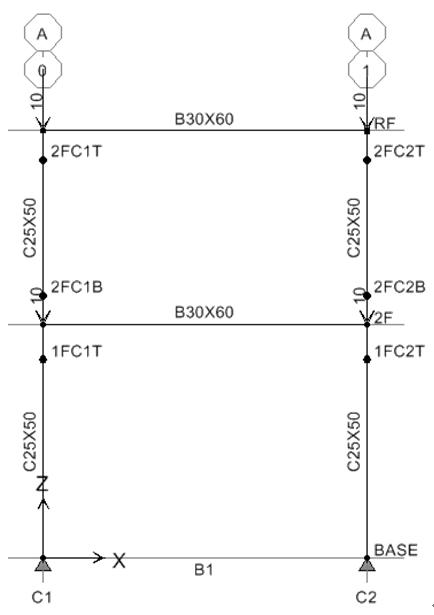 | | 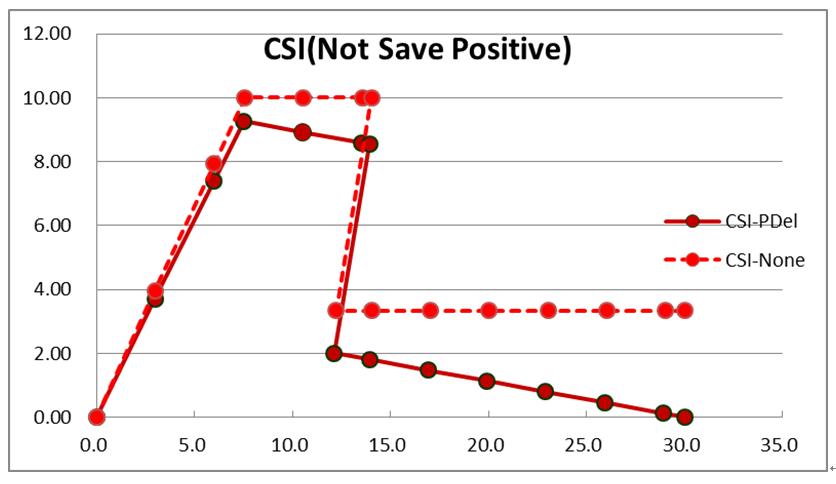 |
| 圖8 雙層門架之結構模型圖(CSI) | | 圖9 雙層門架之容量曲線圖形(CSI) |
比較LCM與CSI等容量曲線如圖10,兩者完全重合,其餘元素降伏破壞發生順序,同本報1235期說明,表示LCM理論驗證可行。
| 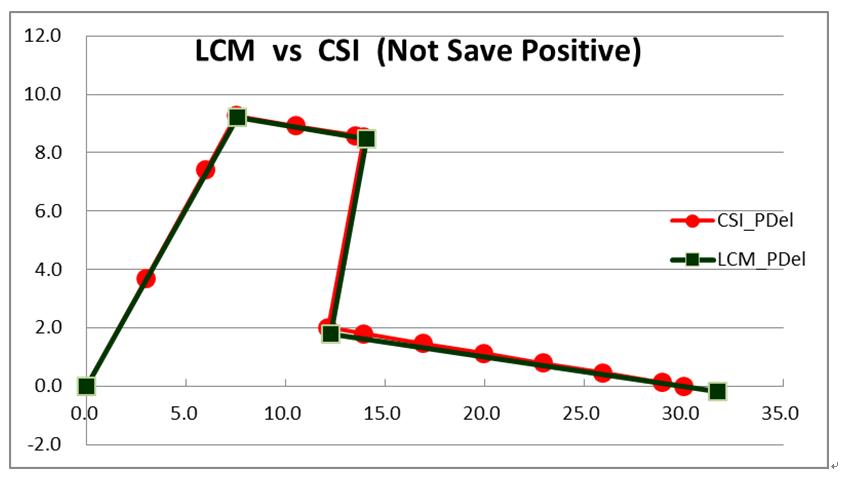 |
| 圖10 雙層門架之LCM與CSI比較 |
最後再舉案例3,說明2F先降伏破壞(同本報1235期中之案例2),僅將1F柱尺寸轉90度與加強其PH外,其餘均同前案例2與前圖6說明,再分別利用LCM與CSI等兩方法求取例門架之容量曲線。
1.LCM(LuChiMan綠奇門)方法:
本例僅列出各階段柱軸力、與P-Delta反向剪力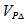 ,分別如表5與6,再合併原始基底剪力Base Shear(本報1235期),得表6最後一列。
,分別如表5與6,再合併原始基底剪力Base Shear(本報1235期),得表6最後一列。
表5 雙層門架之各階段柱軸力
| Drift-RFL | 0 | 1.53 | 1.583 | 1.709 | 3.008 | 6.575 | 8.267 | 8.331 | 22.873 | 23.319 |
| 2FC1_Top | -10 | -6.4 | -6.28 | -5.98 | -5.98 | -7.32 | -7.32 | -8.66 | -8.66 | -8.66 |
| 2FC2_Top | -10 | -13.6 | -13.72 | -14.02 | -14.02 | -12.68 | -12.68 | -11.34 | -11.34 | -11.34 |
| Drift-2FL | 0 | 3.514 | 3.634 | 6.523 | 6.523 | 2.618 | 2.618 | 1.309 | 1.309 | 1.309 |
| 1FC1_Top | -20 | -1.96 | -1.34 | 0.16 | 0.16 | -6.56 | -6.56 | -13.28 | -13.28 | -13.28 |
| 1FC2_Top | -20 | -38.04 | -38.66 | -40.16 | -40.16 | -33.44 | -33.44 | -26.72 | -26.72 | -26.72 |
表6 雙層門架之容量曲線資料
| RFL | Dis.RF | 0 | 5.042 | 5.217 | 8.243 | 9.542 | 9.191 | 10.883 | 9.639 | 24.181 | 24.627 |
| 2FC1_Top | VPD= | 0 | -0.033 | -0.033 | -0.034 | -0.06 | -0.16 | -0.202 | -0.24 | -0.66 | -0.673 |
| 2FC2_Top | VPD= | 0 | -0.069 | -0.072 | -0.08 | -0.141 | -0.278 | -0.349 | -0.315 | -0.865 | -0.881 |
| 1FC1_Top | VPD= | 0 | -0.019 | -0.014 | 0.003 | 0.003 | -0.048 | -0.048 | -0.048 | -0.048 | -0.048 |
| 1FC2_Top | VPD= | 0 | -0.371 | -0.39 | -0.728 | -0.728 | -0.243 | -0.243 | -0.097 | -0.097 | -0.097 |
| BaseShear | VBS= | 0 | 16.11 | 16.66 | 18 | 18 | 12 | 12 | 6 | 6 | 6 |
| BaseShear | VBS+PD= | 0 | 15.62 | 16.15 | 17.16 | 17.07 | 11.27 | 11.16 | 5.3 | 4.33 | 4.3 |
圖11中之淺綠虛線,為原始僅考慮材料非線性之容量曲線(本報1235期),而綠色實線,則其再考慮P-Del效應所得者,可看出因柱頂受壓而水平剪力容量下滑減少趨勢。
 |
| 圖11 雙層門架之容量曲線圖形(LCM) |
2.CSI(ETABS程式)方法:
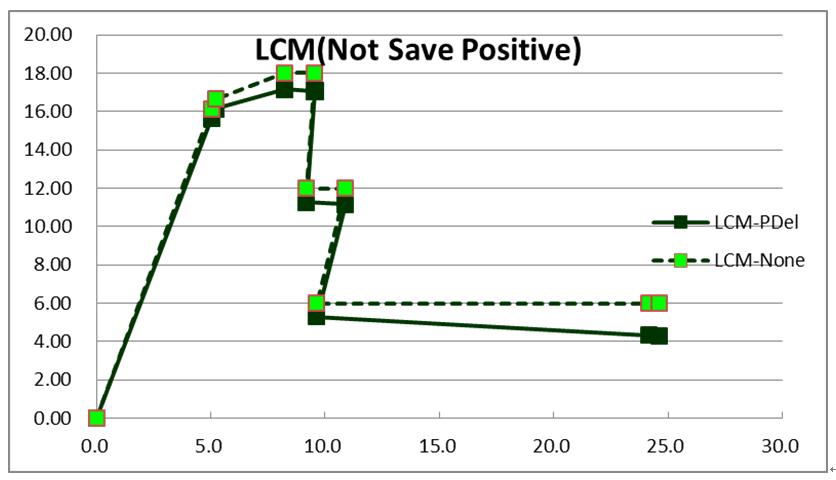
CSI結構模型同前例圖8,側推得門架容量曲線如圖12中之紅色圓形實線,另外紅色圓形虛線,為原始僅考慮材料非線性之容量曲線(本報1235期)。
 |
| 圖12 雙層門架之容量曲線圖形(CSI) |
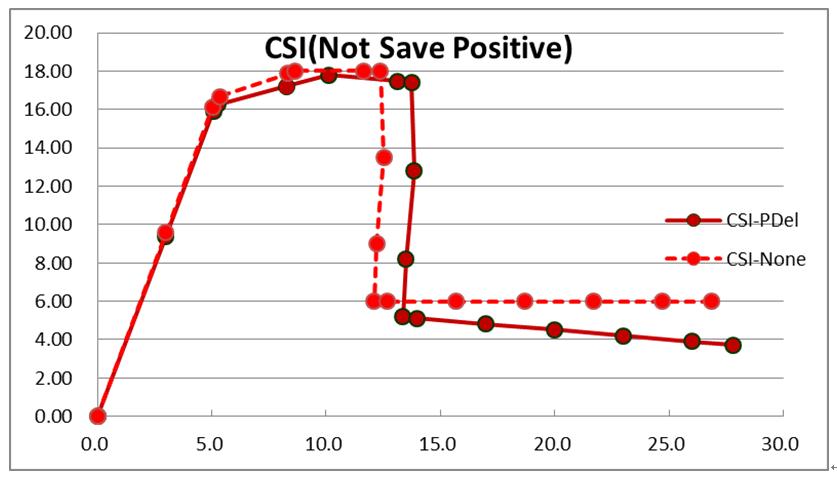
比較LCM與CSI等容量曲線如圖13,可看出兩者因柱頂受壓而水平剪力容量下滑減少趨勢完全相同,至於衰減段部分與元素降伏破壞發生順序,同本報1235說明,表示LCM理論驗證可行。
 |
| 圖13 雙層門架之LCM與CSI比較 |
P-Delta,為軸力乘以側向位移,不是矩形能量,透過矩形能量的轉換,將垂直壓力轉成水平剪力。而在軸力為壓力下,才會減損整體矩形能量,反之拉力則增加。這與人生哲學很像,壓力就像小人,因為小人才會給我們壓力,減損我們的信心能量;拉力像貴人,貴人才會拉我們一把,增加我們正向能量。LCM(LuChiMan綠奇門),所發想的外內力平衡系統之矩形能量(Rectangular Energy)均為矩形,簡單易懂,非線性應用上只要加加減減就好,且可以正確解析外內之變位與力量等結果,並不馬虎(Ref.-1),再一次顯示,矩形能量的可愛之處。
參考文獻
Ref.-1 呂啟明,「矩形能量的可愛1.0-材料與幾何非線性之應用」,Pubu電子書城 或 amazon(亞馬遜,amazon.com),Sep. 2019。
Ref.-2 Computer Structure Inc.,「CSI Analysis Reference Manual」,CSI,July 2010。
Ref.-3 呂啟明,矩形能量應用於材料非線性,技師報第1194期,民國108年10月26日。
Ref.-4 呂啟明,矩形能量應用於材料非線性-以單層門架為例,技師報第1224期,民國109年5月23日。
Ref.-5 呂啟明,矩形能量應用於材料非線性-以雙層門架為例,技師報第1235期,民國109年8月8日。

