矩形能量應用於材料非線性-以雙層門架為例
本報1194期,曾探討矩形能量應用於材料非線性之基本概念;另於本報1224期,舉單層門架例說明矩形能量之應用。茲,再舉雙層門架為例說明不同樓層的相互存在關係,詳圖1。
| 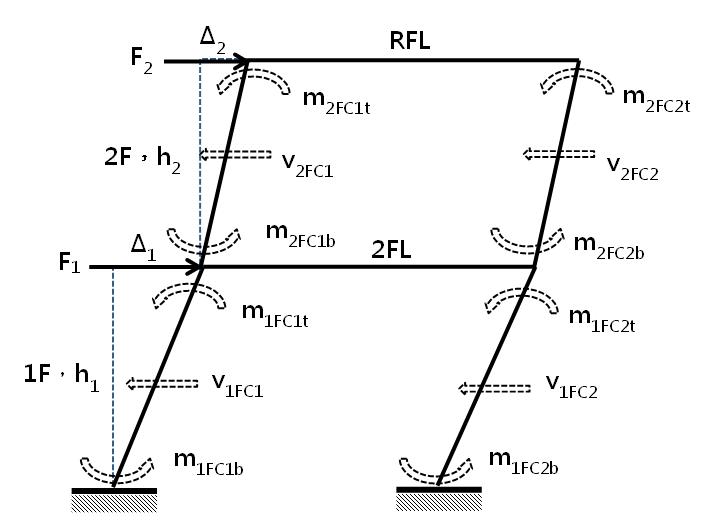 |
| 圖1 雙層單跨門架 |
內外矩形能量說明,同1224期。若取2F柱以上為自由體(Free Body),結果得其如下式1與2,同理再取1F柱以上為自由體,亦可推得內外矩形能量平衡,得下式3與4,餘可參考Ref.-1。

接下來,我們以下圖2之案例1說明,其為一樓高3米6、二樓高3米、跨度5米之對稱雙層單跨柱底鉸接之門架,其中左右柱尺寸均為25x50cm,樑尺寸為30x60cm,彈性模數E值為2.0E+5kgf/cm2,參考樓層側力(floor force)RF與2F分別為2比1,左右兩柱之柱頂與柱底PH分別如下表1。而1F柱底因為鉸接,所以沒有彎矩PH,另外大樑假設強度很大,永遠保持彈性,所以亦沒有PH,本門架即所謂弱柱強樑者。分別利用LCM(LuChiMan綠奇門,Ref.-1)、與CSI (ETABS程式,Ref.-2)等兩方法,求取本例門架之容量曲線(RFL位移與1F基底剪力)。
| 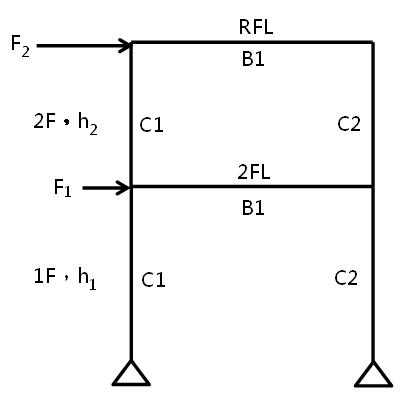 |
| 圖2 案例1之結構系統 |
表1 左右兩柱之PH
| 2FC1top | A | B | C | D | E |
| 2FC2top |
| θ(rad) | 0 | 0 | 0.015 | 0.025 | 0.075 |
| m(t-cm) | 0 | 900 | 900 | 300 | 300 |
| 2FC1bot | A | B | C | D | E |
| 2FC2bot |
| θ(rad) | 0 | 0 | 0.015 | 0.025 | 0.075 |
| m(t-cm) | 0 | 900 | 900 | 300 | 300 |
| 1FC1top | A | B | C | D | E |
| 1FC2top |
| θ(rad) | 0 | 0 | 0.018 | 0.027 | 0.081 |
| m(t-cm) | 0 | 1800 | 1800 | 600 | 600 |
1.LCM(LuChiMan綠奇門)方法
本例參考載重(reference load),由工程師自行指定RF與2F樓層側力分別為2.00與1.00ton,由彈性分析得門架側向位移與基底剪力之關係,如下表2;相關兩柱之彈性分析所得資料,如下表3。其中JBC為柱子彎矩轉自己者(Ref.-1或4),所以為1.00。
表2 彈性分析_門架EB
| Floor | F | V | ratio | Dis. | Δ |
| RFL | 2 | 2 | 0.67 | 2.27 | 0.278 |
| 2FL | 1 | 3 | 1 | 1.992 | 1.992 |
表3 彈性分析_兩柱EB
| Element | Unit | dis/Mref | Kdis | JBC |
| 2FC1_Top | cm | 2.27 | 73.84 | |
| 2FC2_Top | kgf-cm | 167.61 | *1.00 |
| 2FC1_Bot | cm | 2.27 | 58.32 | |
| 2FC2_Bot | kgf-cm | 132.39 | *1.00 |
| 1FC1_Top | cm | 2.27 | 237.89 | |
| 1FC2_Top | kgf-cm | 540 | *1.00 |
應用前述公式,將兩柱之轉角θ與彎矩m,轉成側向變位Δ與水平剪力v,再經彈性修正(Ref.-1),則EB+PH轉換後,如下表4,則各層柱頂與柱底之EB+PH圖形,分別如圖3、4、5中淺藍虛線。
表4 兩柱之EB+PH資料
| Element | Unit | A | B | C | D | E |
| 2FC1_Top | cm | 0 | 12.189 | 16.689 | 11.563 | 26.563 |
| 2FC2_Top | ton | 0 | 3 | 3 | 1 | 1 |
| 2FC1_Bot | cm | 0 | 15.432 | 19.932 | 12.644 | 27.644 |
| 2FC2_Bot | ton | 0 | 3 | 3 | 1 | 1 |
| 1FC1_Top | cm | 0 | 7.566 | 14.046 | 12.247 | 31.687 |
| 1FC1_Top | ton | 0 | 5 | 5 | 1.67 | 1.67 |
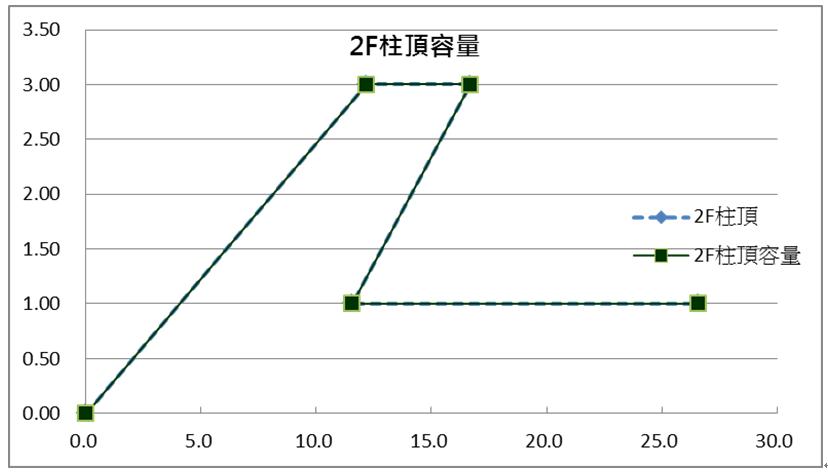 | | 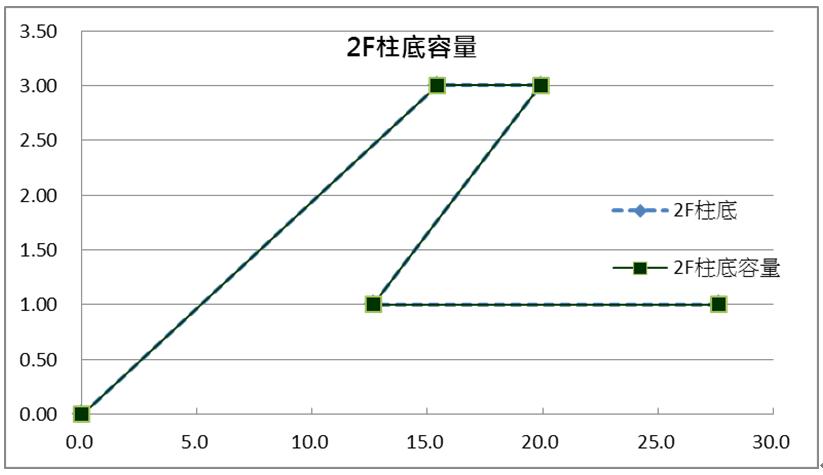 |
| 圖3 2F柱頂EB+PH圖形 | | 圖4 2F柱底EB+PH圖形 |
| | | |
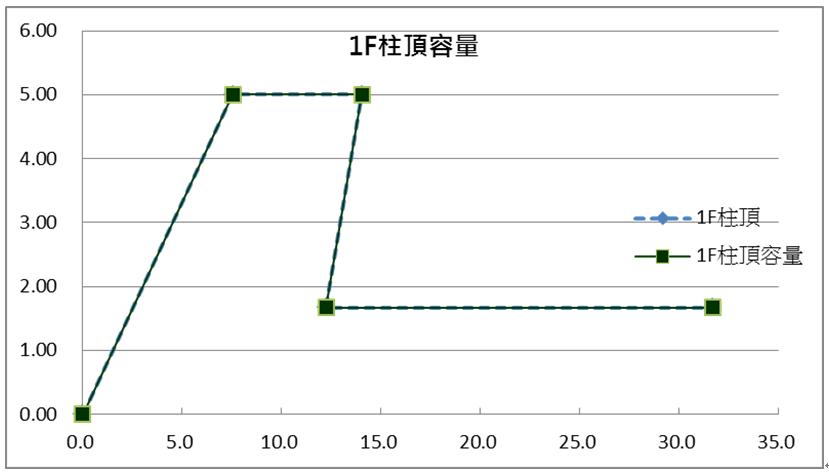 | | |
| 圖5 1F柱頂EB+PH圖形 | | |
節點強度,原則上是樑柱互制取小值者為控制,本例為弱柱強樑,所以柱之強度即代表節點者,如同上表4與上圖3至5,所示之綠色實線,故其與淺藍虛線重合。
樓層容量曲線,以屋頂變位(dis.RF)為樓層位移事件點,將所對應得到節點強度相加,2F與1F等容量曲線資料,得如下表5與6,再將各層容量均轉換到1F者,如圖6中之深藍與深綠等實線,分別表2F與1F之容量,注意其中2F轉換到1F者,需乘以樓層剪力比值1.5 (=3.0/2.0)。再以存正值者(Save Positive)相互比較,可看出1F容量值均小於2F,表示整結構由1F者控制,即降伏破壞均發生在1F柱頂,2F者均保持彈性,即圖6中深綠實線,意為最後求得本例門架之容量曲線。
表5 2F之容量曲線資料
| RF | Dis-RF | 0 | 12.189 | 15.432 | 16.689 | 16.706 | 19.932 | 19.952 | 26.562 | 27.643 |
| 2F-Sum | ΣVi= | 0 | 10.74 | 12 | 12 | 8 | 8 | 4 | 4 | 4 |
| 2FC1_Top | Vi= | 0 | 3 | 3 | 3 | 1 | 1 | 1 | 1 | 1 |
| 2FC2_Top | Vi= | 0 | 3 | 3 | 3 | 1 | 1 | 1 | 1 | 1 |
| 2FC1_Bot | Vi= | 0 | 2.37 | 3 | 3 | 3 | 3 | 1 | 1 | 1 |
| 2FC2_Bot | Vi= | 0 | 2.37 | 3 | 3 | 3 | 3 | 1 | 1 | 1 |
表6 1F之容量曲線資料
| 2FL | Dis-RF | 0 | 7.566 | 14.046 | 14.06 | 31.686 |
| 1F-Sum | ΣVi= | 0 | 10 | 10 | 3.34 | 3.34 |
| 1FC1_Top | Vi= | 0 | 5 | 5 | 1.67 | 1.67 |
| 1FC2_Top | Vi= | 0 | 5 | 5 | 1.67 | 1.67 |
| 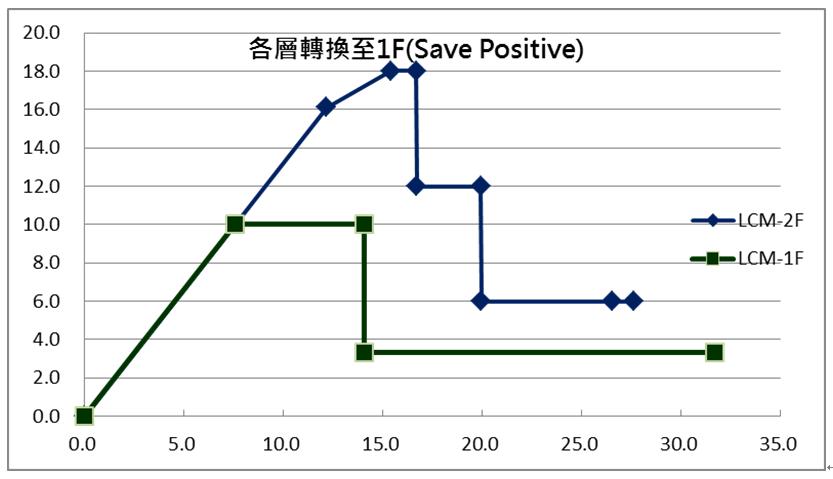 |
| 圖6 各層轉換至1F(Save Positive) |
2.CSI(ETABS程式)方法
CSI結構模型如圖7,參考載重於RFL、2FL,各施加2.0與1.0ton,同前EB與PH等基本資料輸入程式後,先跑彈性分析,再跑側推分析(Pushover),得門架初始降伏與最終破壞等變形,如圖8,再得門架容量曲線,如圖9中之紅色圓形實線。
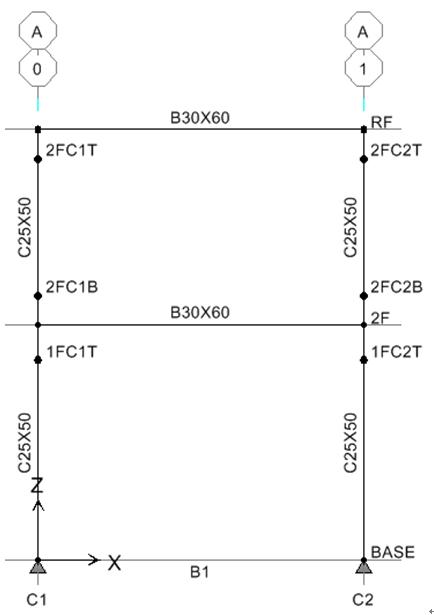 | | 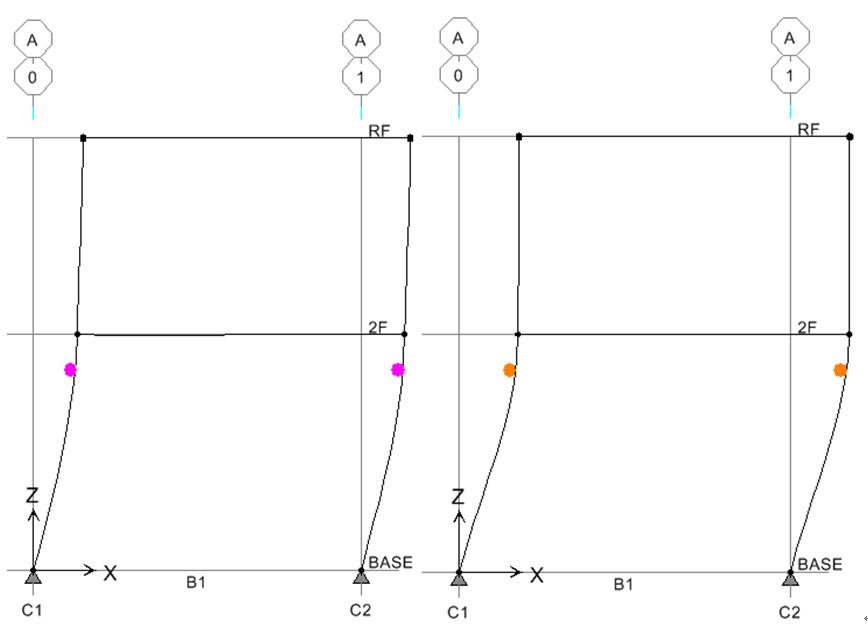 |
| 圖7 結構模型圖(CSI) | | 圖8 初始降伏與最終破壞等變形圖(CSI) |
比較LCM與CSI等容量曲線,如下圖9,兩者完全重合,再者如上圖8,說明1F柱頂先發生降伏,最後亦由1F柱頂發生破壞,2F從頭至尾均保持在線彈性,這與前述LCM方法所得結果相同,表LCM理論驗證可行。
| 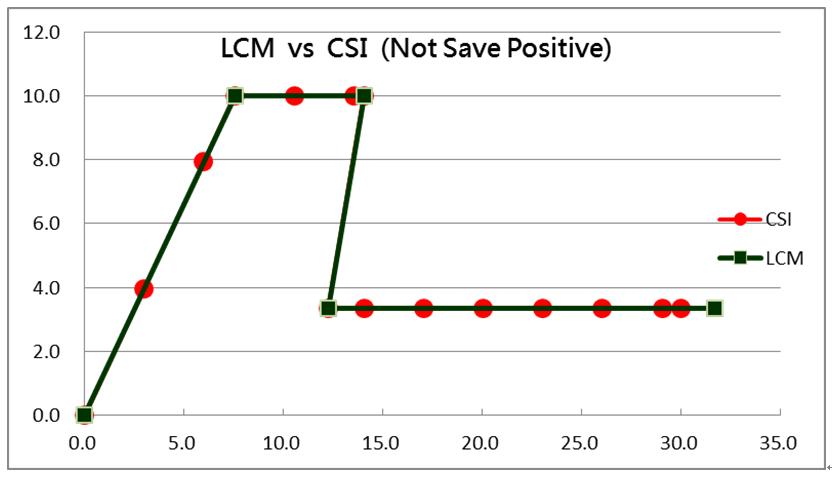 |
| 圖9 LCM與CSI比較(Not Save Positive) |
再舉案例2,同案例1,僅將1F左右柱尺寸轉90度改為50x25cm,並提高1F柱頂之PH如下表7,其餘不變。同樣地,分別利用LCM與CSI等兩方法,求取本例門架之容量曲線。
表7 C1與C2等柱之1F左右柱頂PH
| 1FC1top | A | B | C | D | E |
| θ(rad) | 0 | 0 | 0.018 | 0.027 | 0.081 |
| m(t-cm) | 0 | 3000 | 3600 | 1200 | 1200 |
| 1FC2top | A | B | C | D | E |
| θ(rad) | 0 | 0 | 0.018 | 0.027 | 0.081 |
| m(t-cm) | 0 | 3000 | 3600 | 1200 | 1200 |
1.LCM(LuChiMan綠奇門)方法
同案例1方式,求得2F與1F等容量曲線,再將各層容量均轉換到1F者,如下表8與圖10中之深藍與深綠等實線,分別表2F與1F等容量,可看出2F柱頂先降伏,再來1F柱頂降伏,兩線交點(8.243cm)以後,均由2F柱頂與柱底控制,所以下表9與圖11中深綠實線,意為最後求得本例門架之容量曲線。
表8 2F與1F等容量曲線資料
| RF-dis' | 0 | 5.042 | 6.383 | 9.542 | 9.191 | 10.883 | 9.639 | 24.181 | 24.627 |
| 2F→1F | 0 | 16.11 | 18 | 18 | 12 | 12 | 6 | 6 | 6 |
| RF-dis' | 0 | 5.217 | 12.743 | 11.819 | 31.245 | | | | |
| 1F→1F | 0 | 16.66 | 20 | 6.66 | 6.66 | | | | |
| 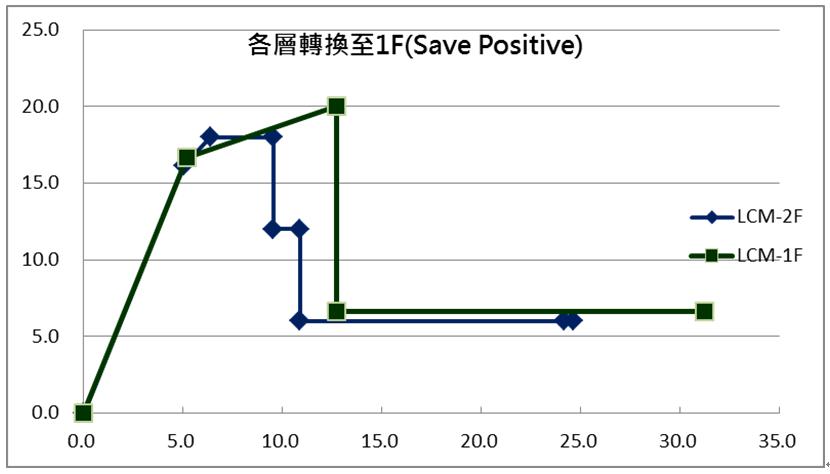 |
| 圖10 各層轉換至1F(Save Positive) |
表9 案例2整體容量曲線資料
| 破壞點 | 原點 | 2F柱頂 | 1F柱頂 | 交點 | 2F柱頂 | 2F柱頂 | 2F柱底 | 2F柱底 | 2F柱頂 | 2F柱底 |
| Dis.RF | 0 | 5.042 | 5.217 | 8.243 | 9.542 | 9.191 | 10.883 | 9.639 | 24.181 | 24.627 |
| 1F→1F | 0 | 16.11 | 16.66 | 18 | 18 | 12 | 12 | 6 | 6 | 6 |
| 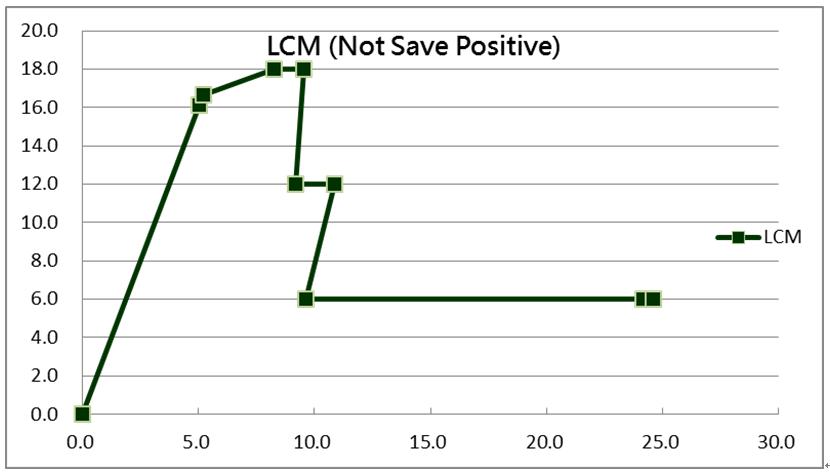 |
| 圖11 案例2整體容量曲線資料(Not Save Positive) |
2.CSI(ETABS程式)方法
同案例1,先跑彈性分析再跑側推分析,得門架初始降伏與最終破壞等變形,如圖12,再得門架容量曲線,如圖13中之紅色圓形實線。
| 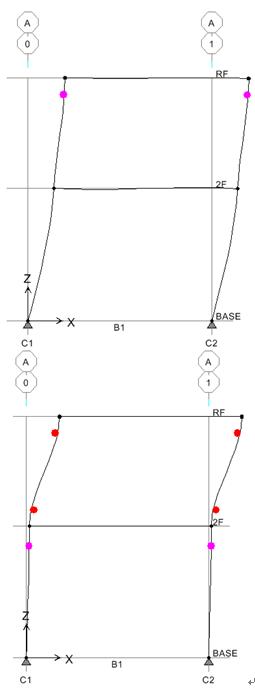 |
| 圖12 初始降伏與最終破壞等變形圖(CSI) |
比較LCM與CSI等容量曲線,如下圖13,兩者除衰減段外,幾乎完全重合,再如上圖12,說明2F柱頂先發生降伏、最後亦由2F柱頂與柱底發生破壞時,1F柱頂從頭至尾,均保持在降伏段未進入衰減段,這與前述LCM方法所得結果相同;而下降段不同原因,CSI卸載方式之變位,為對應求得非理論解析,且並無考慮1F與2F交點(8.243cm)後樓層互制,所以其變位接近LCM求得1F者,如圖10之綠色實線,所以LCM理論驗證可行並優於CSI。
| 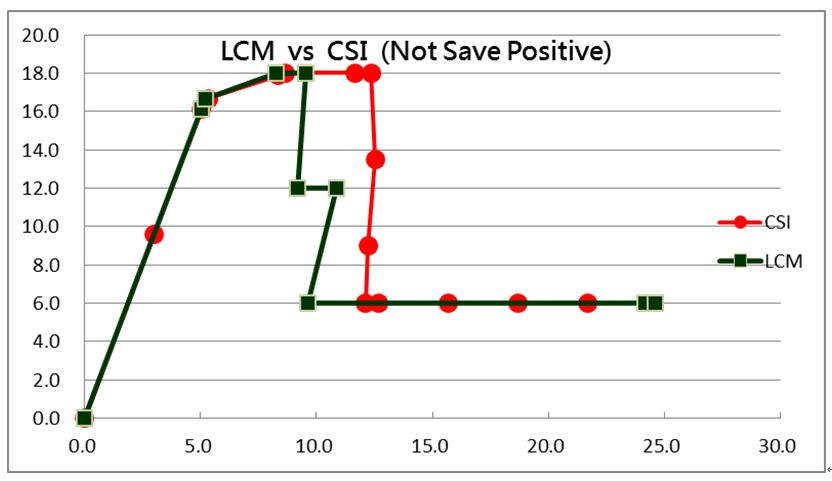 |
| 圖13 LCM與CSI比較 |
綜合本報1194與1124等期探討,LCM(LuChiMan綠奇門)所發想的外內力平衡系統之矩形能量(Rectangular Energy)均為矩形,簡單易懂;非線性應用上,只要加加減減就好,且可以正確解析外內之變位與力量等結果,並不馬虎(Ref.-1),且優於CSI卸載中變位僅對應無互制,再一次顯示矩形能量的可愛之處。
參考文獻
Ref.-1 呂啟明,「矩形能量的可愛1.0-材料與幾何非線性之應用」,Pubu電子書城 或 amazon(亞馬遜,amazon.com),Sep. 2019。
Ref.-2 Computer Structure Inc.,「CSI Analysis Reference Manual」,CSI,July 2010。
Ref.-3 呂啟明,矩形能量應用於材料非線性,技師報第1194期,民國108年10月26日。
Ref.-4 呂啟明,矩形能量應用於材料非線性-以單層門架為例,技師報第1224期,民國109年5月23日。

